Integrales para amar las matemáticas, conoce 6 formas de integración más usados

El término «integrales» puede referirse a varios conceptos diferentes en las matemáticas. El significado más común es el objeto fundamental del cálculo correspondiente a la suma de piezas infinitesimales para encontrar el contenido de una región continua.

Otros usos de «integral» incluyen valores que siempre toman valores enteros (p. Ej., Incrustación integral, gráfico integral ), objetos matemáticos para los que los números enteros forman ejemplos básicos (p. Ej., Dominio integral ) y valores particulares de una ecuación (p. Ej., Curva integral).

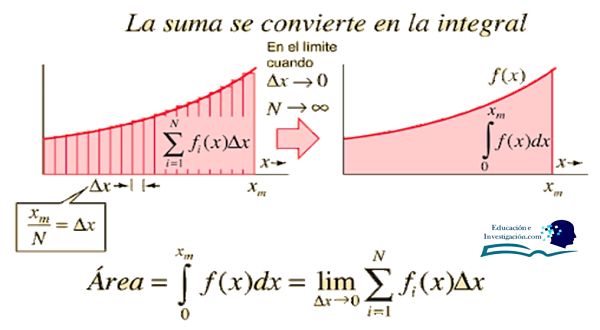
En cálculo, una integral es un objeto matemático que puede interpretarse como un área o una generalización de un área. Además de las integrales, están las derivadas, es el elemento fundamental del cálculo.

En tal sentido, con integral admiten antiderivada y primitiva. La forma de hallar una integral se conoce como integración (una frase más antigua para la integración es cuadratura), y el valor o cálculo aproximado de una integral se denomina integración numérica.

1.- Integrales de Riemann

La integral de Riemann es la definición integral más simple y la única que se encuentra generalmente en física y cálculo elemental. Desde luego, según el autor Jeffreys (1988, p. 29), «parece que los casos en los que estos métodos [es decir, generalizaciones de la integral de Riemann] son aplicables y la [definición de integral de Riemann] no lo es, son demasiado raros en física para compensar la dificultad extra».

La integral de Riemann de la función más de la que está escrito

(1)

Tenga en cuenta que si , la integral se escribe simplemente

(2)

en contraposición a .

2.- Integrales Lebesgue

Cada definición de integral se basa en una medida particular . Por ejemplo, la integral de Riemann se basa en la medida de Jordan y la integral de Lebesgue se basa en la medida de Lebesgue.

Además, dependiendo del contexto, se puede usar cualquiera de una variedad de otras notaciones integrales.

Por ejemplo, la integral de Lebesgue de una función integrable sobre un conjunto que es medible con respecto a una medida se escribe a menudo.

(3)

3.- Integrales Stieltjes

En el caso de que el conjunto , sea un intervalo , generalmente se adopta la notación «subíndice-superíndice» de ( 2 ).

De hecho, otra generalización de la integral de Riemann es la integral de Stieltjes, donde la función integrando definida en un intervalo cerrado puede integrarse contra una función acotada de valor real definida en I, cuyo resultado tiene la forma

(4)

o equivalente

(5)

Otro escenario más en el que la notación puede cambiar se produce en el estudio de la geometría diferencial , en el que el integrando se considera una forma k diferencial más general y se puede integrar en un conjunto utilizando cualquiera de las notaciones equivalentes.

(6)

donde es la medida de Lebesgue antes mencionada. Cabe señalar que la notación en el lado izquierdo de la ecuación () es similar a la de la expresión () anterior.

Hay dos clases de integrales (de Riemann): integrales definidas como ( 5 ), que tienen límites superior e inferior, e integrales indefinidas, como

(7)

que están escritos sin límites.

Tal vez estos temas te puedan interesar

4.- Integrales Definidas

El primer teorema fundamental del cálculo permite calcular integrales definidas en términos de integrales indefinidas , ya que si es la integral indefinida de , entonces

(8)

Es más, el primer teorema fundamental del cálculo se puede reescribir de manera más general en términos de formas diferenciales (como en () arriba) para decir que la integral de una forma diferencial sobre el límite de alguna variedad orientable es igual a la derivada exterior de sobre el interior de , es decir,

(9)

Escrito de esta forma, el primer teorema fundamental del cálculo se conoce como Teorema de Stokes.

Como ya es sabido, la derivada de una constante es cero, por ello, en cuanto a los integrales indefinidas se definen solo hasta una constante arbitraria de integración , es decir, quedando así la integral.

(10)

Para la mayoría de los amantes de las matemáticas les puede resultar muy útil, diferenciar integrales conduce a algunas identidades útiles y poderosas. Por ejemplo, si es continuo, entonces

(11)

que es el primer teorema fundamental del cálculo. Otras identidades derivadas-integrales incluyen

(12)

5.- Integrales Leibniz

la regla integral de Leibniz

(13)

(Kaplan 1992, p. 275), su generalización

(14)

(Kaplan 1992, p. 258), y

(15)

como se puede ver aplicando ( 14 ) en el lado izquierdo de ( 15 ) y usando integración parcial.

Otras identidades integrales incluyen

(dieciséis)

(17)

			(18)
			(19)

y la divertida identidad integral

(20)

donde está cualquier función y

(21)

siempre que y sea real (Glasser 1983).

6.- integrales con exponentes racionales

Las integrales con exponentes racionales a menudo se pueden resolver haciendo la sustitución , donde es el mínimo común múltiplo del denominador de los exponentes.

REFERENCIAS:

Beyer, W. H. «Integrales». CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, págs. 233-296, 1987.
Boros, G. y Moll, V. Integrales irresistibles: simbólica, análisis y experimentos en la evaluación de integrales. Cambridge, Inglaterra: Cambridge University Press, 2004.
Bronstein, M. Integración simbólica I: Funciones trascendentales. Nueva York: Springer-Verlag, 1996.
Dubuque, W. G. «Re: Integrales hechas gratis en la Web». publicación en math-fun@cs.arizona.edu , 24 de septiembre de 1996.
Glasser, M. L. «Una propiedad notable de las integrales definidas». Matemáticas. Computación. 40 , 561-563, 1983.
Gordon, R. A. Las integrales de Lebesgue, Denjoy, Perron y Henstock. Providence, RI: Amer. Matemáticas. Soc., 1994.
Gradshteyn, I. S. y Ryzhik, I. M. Tablas de integrales, series y productos, 6ª ed. San Diego, CA: Academic Press, 2000.
Jeffreys, H. y Jeffreys, B. S. Métodos de física matemática, 3ª ed. Cambridge, Inglaterra: Cambridge University Press, pág. 29 de 1988.
Kaplan, W. Cálculo avanzado, 4ª ed. Reading, MA: Addison-Wesley, 1992.
Piessens, R .; de Doncker, E .; Uberhuber, C. W .; y Kahaner, D. K. QUADPACK: Un paquete de subrutinas para la integración automática. Nueva York: Springer-Verlag, 1983.
Ritt, J. F. Integración en términos finitos: teoría de métodos elementales de Liouville. Nueva York: Columbia University Press, pág. 37, 1948.
Shanks, D. Problemas resueltos y no resueltos en teoría de números, 4ª ed. Nueva York: Chelsea, pág. 145, 1993.

¡Si te pareció interesante este artículo, déjamelo saber!

Te gustaría ser parte de mi grupo público de Facebook, en el que todos pueden participar, dejando comentarios, compartiendo fotos de sus trabajos e inclusive haciendo preguntas abiertas y similares.

¡Haz Clic en el botón con la manito y nos vemos dentro!