Lanzamiento Horizontal: ¿Qué es?, Características, Fórmulas y 5 Ejercicios

En el vasto campo de la física, el lanzamiento horizontal es un concepto fundamental que se encuentra en muchas situaciones de la vida cotidiana, desde el deporte hasta la ingeniería.

En este post, exploraremos qué es exactamente el tiro horizontal, ¿Qué es?, Características, fórmulas y 5 ejercicios resueltos.

Además, cómo se relaciona con otros principios físicos y cómo podemos aplicarlo en diferentes contextos.

¿Qué es el lanzamiento horizontal?

El lanzamiento horizontal que también es conocido como tiro horizontal, es un concepto de la física, que describe el movimiento de un objeto que es lanzado horizontalmente desde una altura determinada.

Además, con una velocidad inicial en la dirección horizontal, es decir, paralela a la superficie de la tierra.

Por lo que se puede decir, que durante su trayectoria, el objeto experimenta únicamente la aceleración debido a la gravedad, que actúa verticalmente hacia abajo.

De hecho, su velocidad horizontal permanece constante, siempre y cuando no haya fuerzas externas actuando sobre él.

Ejemplo del lanzamiento horizontal

Imagina que lanzas una pelota desde lo alto de un edificio con una velocidad horizontal inicial de 10 m/s. La pelota cae verticalmente debido a la gravedad, pero su velocidad horizontal permanece constante.

Suponiendo que no hay resistencia del aire u otras fuerzas externas significativas, la pelota seguirá moviéndose horizontalmente a 10 m/s mientras cae verticalmente hasta el suelo. Este movimiento combinado de caída vertical y movimiento horizontal constituye un lanzamiento horizontal.

Características del tiro horizontal

Este tipo de movimiento, es muy interesante de estudiar, ya que las consideraciones dinámicas presentes, nos garantizan una mejor comprensión de un evento que guarde relación al lanzamiento de cualquier objeto en el plano horizontal.

Por lo que, estas son las 7 características más comunes:

• Debe partir con una velocidad inicial en dirección horizontal.
• La velocidad inicial es igual que el componente de la velocidad en el plano horizontal o eje X, es decir, Vo = Vx.
• La velocidad Vx es constante durante todo el recorrido, o en cualquier instante de tiempo.
• La velocidad Vy varía en cada instante de tiempo, debido a la aceleración de la gravedad.
• El alcance del cuerpo en llegar al suelo depende de la magnitud de la velocidad en el eje «X» y del tiempo de vuelo.
• La velocidad real en cualquier instante de tiempo, se determina con las componentes vertical y horizontal de la velocidad.
• La altura total del lugar del que se lanza o dispara el objeto, se puede determinar con la aceleración de gravedad y del tiempo de vuelo. Por otro lado, también se puede obtener conociendo la velocidad en el eje «Y».

Fórmulas de tiro horizontal

Las fórmulas del lanzamiento o tiro horizontal, son los recursos que se necesitan en un práctico. Por lo que, los conceptos y características dan sustento para sus hipótesis. A continuación una explicación detallada de las fórmulas y luego verás el resumen de todas.

• Componente de la velocidad «Vx»

La velocidad horizontal de un objeto (Vx), en un tiro horizontal es constante y se mantiene durante todo el movimiento. Si no hay fuerzas horizontales actuando sobre el objeto, esta velocidad es la misma que la velocidad inicial total del lanzamiento (Vo). Quedando así:

Vx = Vo 

• Componente de la velocidad «Vy»

La velocidad vertical de un objeto (Vy), en un tiro horizontal es variable en cada instante de tiempo durante el movimiento en el aire. Varía en proporción directa de la fuerza de aceleración de gravedad (g). Quedando así:

Vy = g . t  (En función del tiempo)

Vy ² = 2 . g . y (En función de la Altura)

• Altura del lugar del lanzamiento «Yt»

Yt = g . tv ² / 2    (Yt es altura total y Tv es el tiempo de vuelo)

• Altura que ha descendido en un instante de tiempo «Y»

Y = g . t ² / 2  (Es idéntica a la anterior fórmula, con la diferencia de que el tiempo es otro)

• Tiempo de Vuelo «Tv»

El tiempo de vuelo, es el período que dura el objeto en el aire desde su lanzamiento, hasta alcanzar el suelo.

Tv ² =  2 . Yt  / g  (Raíz cuadrada de dos por la altura total y divido entre gravedad)

• Alcance horizontal «R»

El alcance horizontal, es la distancia que puede lograr un objeto físico desde el punto del lanzamiento; pero, en el eje X hasta donde llega a tocar el suelo. Tiene por ecuación la siguiente expresión:

R = Vx . Tv (Corresponde a la distancia máxima en el eje X)

• Velocidad real o resultante «VR»

La velocidad real o resultante de este tipo de movimiento semi parabólico en cualquier instante de tiempo, se determina con la siguiente ecuación de pitágoras:

VR ² =  Vx ² + Vy ²  (VR es el el vector de la velocidad resultante en un instante de tiempo)

• Componentes del vector posición «dr», «dx», «dy»

Si un cuerpo tiene un movimiento compuesto, cada uno de sus movimientos componentes actúa como si los demás no existieran.

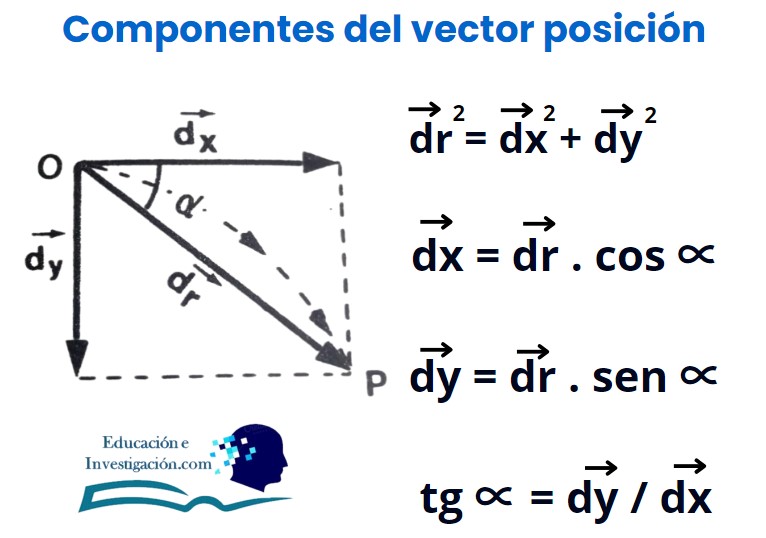
Resumen de fórmulas para el lanzamiento horizontal

Tener las ecuaciones a la mano y de algún modo organizadas, te da la ventaja a la hora de practicar e internalizar sus significados, procedimientos y logar resultados deseados.

Por lo que, a continuación te dejo una lista de las fórmulas agregando con ello, el símbolo, significado y sus unidades.

Principios físicos involucrados con el movimiento de proyectiles

Es fundamental conocer los principios físicos que gobiernan el lanzamiento horizontal. Por ello, Hablaremos sobre la ley de la inercia, la influencia de la gravedad y la ausencia de fuerzas verticales durante el movimiento horizontal.

También discutiremos cómo estos principios se aplican en la práctica y cómo pueden ser útiles en la resolución de problemas.

Ley de la inercia en el tiro horizontal

La ley de la inercia, como parte de los principios fundamentales de la física, se aplica al tiro horizontal de la siguiente manera:

• Cuando un objeto se mueve horizontalmente a una velocidad constante, continuará moviéndose a esa velocidad a menos que una fuerza externa actúe sobre él.

Por tal razón, en el tiro horizontal, un objeto proyectado horizontalmente con una velocidad inicial permanecerá en movimiento horizontal a esa velocidad constante debido a la falta de fuerzas de fricción significativas en el aire en la dirección horizontal.

En resumen, la ley de la inercia indica que un objeto en movimiento horizontal seguirá moviéndose horizontalmente a menos que se le aplique una fuerza externa que lo detenga o cambie su velocidad.

Influencia de la gravedad

En el lanzamiento horizontal, la influencia de la gravedad se limita a la trayectoria vertical del objeto. Aunque el objeto se proyecta inicialmente con una velocidad horizontal constante, la gravedad actúa verticalmente, haciendo que el objeto caiga con el tiempo.

Sin embargo, al no existir fuerzas horizontales significativas que contrarresten el movimiento, la velocidad horizontal permanece constante. En consecuencia, la gravedad afecta la trayectoria vertical pero no la horizontal en este tipo de lanzamiento.

Aplicaciones prácticas del lanzamiento horizontal

Las aplicaciones nos llevan a explorar algunas en el plano real sobre el lanzamiento horizontal en diferentes campos.

Desde el lanzamiento de proyectiles en la física clásica hasta el diseño de trayectorias de vuelo en la ingeniería aeroespacial, veremos cómo este concepto es fundamental en numerosas áreas de estudio y trabajo.

Ejemplos:

1. Deportes de precisión: En deportes como el tiro con arco o el lanzamiento de precisión en atletismo, se aplican los principios del lanzamiento horizontal para alcanzar objetivos específicos. Por ejemplo, en el tiro con arco, los arqueros ajustan el ángulo y la fuerza de su lanzamiento horizontalmente para alcanzar el blanco con la máxima precisión.
2. Diseño de rampas de acceso: En arquitectura y diseño urbano, el lanzamiento horizontal se considera al diseñar rampas de acceso para personas con discapacidades. La pendiente y la longitud de estas rampas se calculan cuidadosamente para garantizar que los usuarios puedan subir o bajar con comodidad y seguridad, utilizando el mínimo esfuerzo posible. La aplicación de los principios del lanzamiento horizontal ayuda a crear accesibilidad para todos en entornos urbanos y arquitectónicos.

Consejos para el estudio y la práctica

Para aquellos interesados en aprender más sobre el lanzamiento horizontal o mejorar sus habilidades en este ámbito, ofreceremos algunos consejos útiles para el estudio y la práctica.

Esto puede incluir recursos de aprendizaje recomendados, ejercicios prácticos y herramientas útiles para la simulación y la visualización del movimiento horizontal.

5 Ejercicios resueltos del lanzamiento horizontal

Problema 1

Un jugador de béisbol arroja una pelota horizontalmente desde lo alto de un montículo, dicha pelota posee una velocidad de 35 m/s, se pide calcular, la distancia horizontal y vertical a los 0.5 segundos de caída. 

Solución: Recordemos que al ser un tiro horizontal, la velocidad vertical no existe, solo tendremos una velocidad inicial en «Vx» que es de 35 m/s, ahora si nos piden calcular la distancia horizontal y vertical, en determinado tiempo, podemos resolverlo con 2 fórmulas.

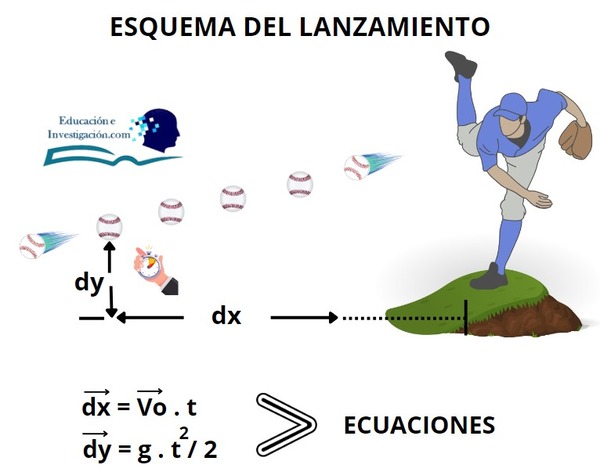
Procedemos a resolver el ejercicio partiendo de los datos e interrogantes.

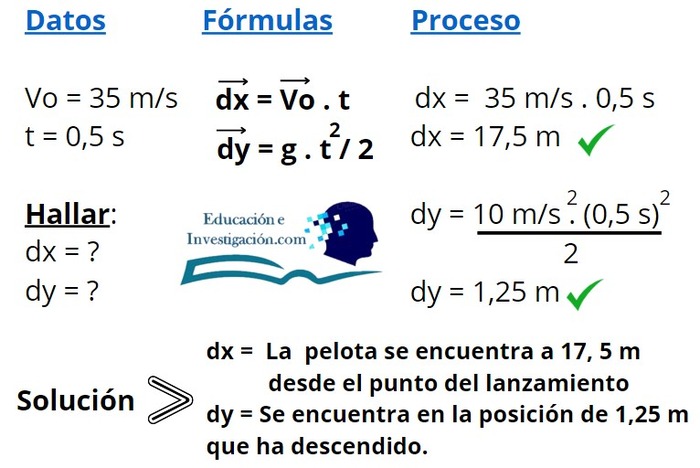
Problema 2

Un motociclista salta horizontalmente con una velocidad inicial de 40 m/s, la altura de la rampa desde la que salta es de 80 metros arriba del punto de contacto, calcule a) ¿Cuánto tiempo permanece en el aire el motociclista? b) ¿Cuán lejos viajó horizontalmente? , c) Sus componentes horizontal y vertical de velocidad.

Solución: Bien, nuevamente continuaremos haciendo uso de las fórmulas para la respuesta de éste problema, así que sigue el paso a paso con atención.

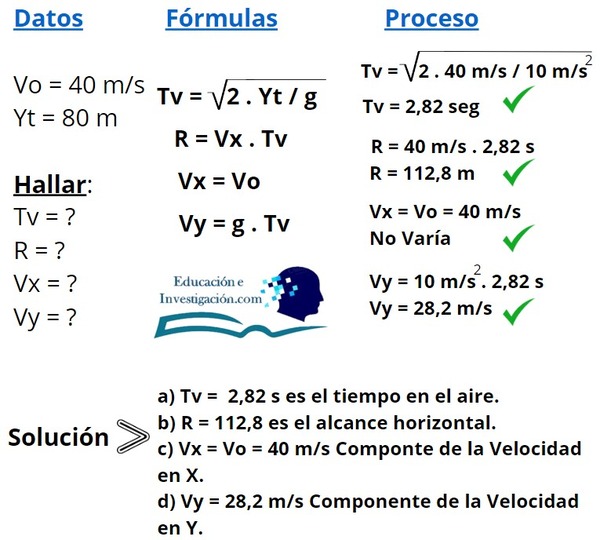
Problema 3

Un jugador golpea horizontalmente una pelota, desde la parte superior de un edificio de 12 metros de altura, la velocidad inicial con la que sale la pelota es de 8 m/s. Calcular: a) el tiempo hasta llegar al suelo; b) la distancia que cae de la base del edificio hasta donde toca la pelota al suelo; c) componente horizontal y vertical al tocar el suelo.

Solución: Nuevamente aplicaremos las fórmulas antes mencionadas, es similar al anterior solo que ésta vez lo haremos más directo. 

Problema 4

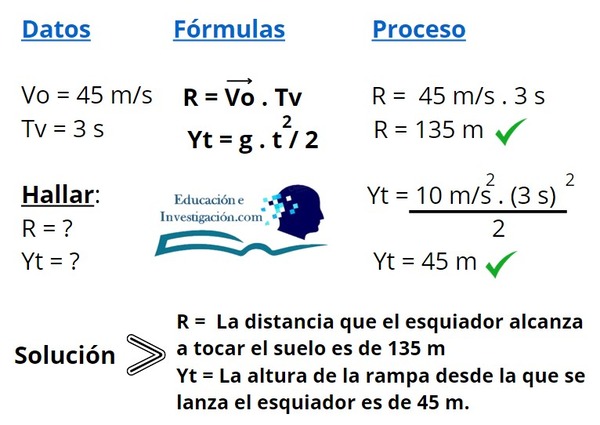
Un esquiador salta horizontalmente con una velocidad inicial de 45 m/s, se sabe que tarda 3 segundos en llegar al suelo de la nieve. Calcule a) ¿Cuán lejos viajó horizontalmente? y ¿Cuánto mide la altura de la rampa?

Solución: Bien, nuevamente continuaremos haciendo uso de las fórmulas para la respuesta de éste problema, así que sigue el paso a paso con atención.

Problema 5

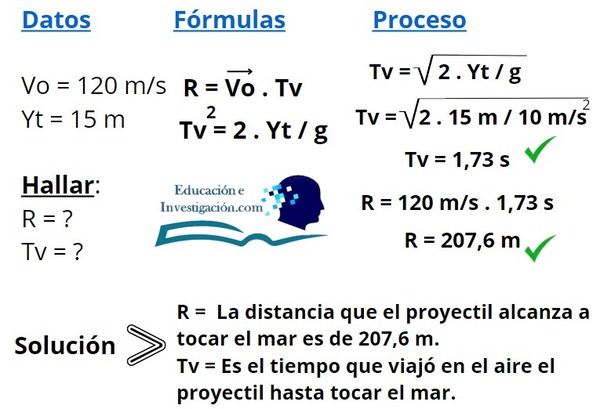
Desde un barco de guerra es lanzado un proyectil, y el cañón está situado a 15 m sobre el mar, con una velocidad de 120 m/s. Se desea saber: a) ¿Qué alcance tendrá el proyectil?; b) ¿En cuánto tiempo alcanza a tocar el mar?

Solución: Bien, continuaremos haciendo uso de las fórmulas para la respuesta de éste problema, así que sigue el paso a paso con atención.

Conclusión

El lanzamiento horizontal es un concepto fascinante que se encuentra en el corazón de muchos fenómenos físicos y aplicaciones prácticas.

Al comprender sus fundamentos y principios, podemos desarrollar una apreciación más profunda del mundo que nos rodea y aprovechar su potencial en diversas áreas de estudio y trabajo.

Antes de culminar, quería recordarte que en el artículo pasado estaba hablando sobre el Lanzamiento Inclinado, si aún no lo haz leído, acá te voy a dejar el enlace para que lo leas, te puede interesar:

Preguntas Frecuentes ⭐​⭐​⭐​

¡Bienvenido a nuestra sección de preguntas frecuentes sobre el lanzamiento horizontal!

¿Alguna vez te has preguntado cómo se aplican los principios del lanzamiento horizontal en diferentes áreas de la vida? ¿O qué aplicaciones prácticas tiene en campos como la física, el deporte o la ingeniería?

¡Estás en el lugar correcto para encontrar respuestas claras y concisas! Sigue leyendo para descubrir más sobre este fascinante concepto y comparte tus conocimientos en redes sociales para que otros también puedan aprender.

¡Vamos a explorar juntos!