La magnitud en física >> es uno de los temas más comunes cuando al referirnos a cantidades y medidas asociadas a unidades, están muy presentes en cada una de las ramas de estudio que la forma.
Al mismo tiempo, las magnitudes fundamentales de la física están englobadas dentro de tres tipos y por lo cual, se convierten en parte del lenguaje universal con el que se pueden representar las cantidades o valores dentro de un fenómeno físico.
Tal vez, muchas personas que recién están estudiando en bachillerato o en universidades querrán saber, para que sirven en el análisis dimensional.
¿Qué es la magnitud en Física?
En el campo de la física, entendemos por magnitud un conjunto de propiedades que pueden medirse. Así, un resultado puede expresarse mediante un número y una unidad.
En otras palabras, todo lo que se puede medir tiene una magnitud. Una longitud, una temperatura, una corriente, una masa, una cantidad de materia.
3 Tipos de Magnitudes Fundamentales de la Física
La magnitud en física, aparece cuando medimos con diferentes instrumentos dichas propiedades fundamentales; en consecuencia, todas se pueden resumir en 3 grandes grupos, los cuáles llamaremos:
- Longitud, se refiere a todas las propiedades que tengan que ver con medidas unidimensionales, bidimensionales y tridimensionales. Siendo la principal en el sistema MKS, el «Metro», en el sistema sistema CGS, el «Centímetro»
- Masa, esta magnitud corresponde a todos los cuerpos que se les mide la cantidad de masa o materia que poseen en determinados múltiplos y submúltiplos. Siendo la principal en el sistema MKS, el «Kilogramo», en el sistema sistema CGS, el «Gramos»
- Tiempo, es la magnitud que corresponde al período en el que transcurren los fenómenos y este es invariable y no depende de ningún otro factor, por lo que el tiempo es una magnitud de referencia para el análisis del movimiento de los cuerpos. Siendo la principal en el sistema MKS, el «Segundo», en el sistema sistema CGS, el «Segundo».

He de aclarar, que no son las únicas magnitudes fundamentales que se estudian en la física, pero las tres anteriores que te he mencionado, son las más empleadas en el análisis dimensional o del estudio del movimiento de los cuerpos.
¿Cómo se mide una magnitud en física?
Para medir una cantidad, hay que compararla con otra del mismo tipo llamada unidad. También tienes que ver cuántas veces está incluida esa unidad en la cantidad que estás midiendo.
Por ejemplo, si intenta medir la longitud de una mesa (magnitud en física), primero tiene que elegir una unidad de medida.
A continuación, se observa la frecuencia con la que esta unidad está contenida en la cantidad que se desea medir. Por lo tanto, el resultado de esta medición debe ser el resultado numérico y la unidad que se utilizó en la medición.
A pesar del inconmensurable número de cantidades y de la gran variedad de unidades que podemos utilizar para medirlas. La medición de cualquier cantidad puede reducirse a un número realmente pequeño de cantidades denominadas cantidades básicas.
Sistema Internacional de Unidades (SI)
El Sistema Internacional de Unidades (SI), creado en 1960, es el sistema mundialmente aceptado. Se basa en el sistema métrico decimal y consta de siete cantidades básicas.
A ellas se añaden sus correspondientes unidades de medida. Todas se basan en fenómenos físicos fundamentales, excepto la unidad de masa: el kilogramo.
Tamaño básico
Símbolo Unidad de medida Símbolo Símbolo
Longitud L Metros m
Masa M Kilogramo kg
Tiempo T Segundo s
Corriente I Amperio A
Temperatura T Kelvin K
Cantidad de sustancia N Moles mol
Intensidad luminosa J candela cd
¿Para qué sirve la magnitud en física con respecto al análisis dimensional?
La ecuación dimensional, puede utilizarse para determinar la unidad de medida de la cantidad considerada. Por ejemplo, puede derivarse de la ecuación dimensional de la fuerza. La unidad de fuerza en EE.UU. es Newton (N). En resumen, N = kg. m / s2.
También puede utilizarse para comprobar si una ecuación es correcta o incorrecta. Esto se debe a que la ecuación debe ser homogénea en términos de dimensiones. En cualquier caso, ambos miembros deben tener la misma ecuación dimensional.
- El análisis dimensional, es la base de los ensayos de modelos a pequeña escala que se utilizan en muchos ámbitos de la ingeniería, como la aeroespacial, la automoción y la ingeniería civil.
- Estas pruebas proporcionan información sobre lo que ocurre en el fenómeno a escala real cuando existe una similitud física entre el fenómeno real y la prueba. Esto se debe a que los resultados obtenidos en un modelo a escala reducida también se aplican al modelo a escala real.
- Por ejemplo, si los números adimensionales que se utilizan como variables independientes para la prueba tienen el mismo valor en el modelo.
>> Te interesan los movimientos rectilíneos variados, este artículo te va ayudar con teoría y práctica.
Movimiento Rectilíneo Uniformemente Variado; Física de 4to año 🎯
Magnitudes escalares y vectoriales
Dentro de la magnitud en física, tenemos la gran variedad de cosas medibles (magnitudes) puede clasificarse y dividirse en dos grandes grupos:
– Magnitudes escalares, que sólo pueden tener un único valor. Por ejemplo: 50 g, o 54,65 s, se denominan magnitudes escalares. Esto se debe a que se determinan con un número y su unidad correspondiente.
– Magnitudes vectoriales, que deben conocerse para poder enunciarlas correctamente: Su valor o módulo, su dirección y su sentido.
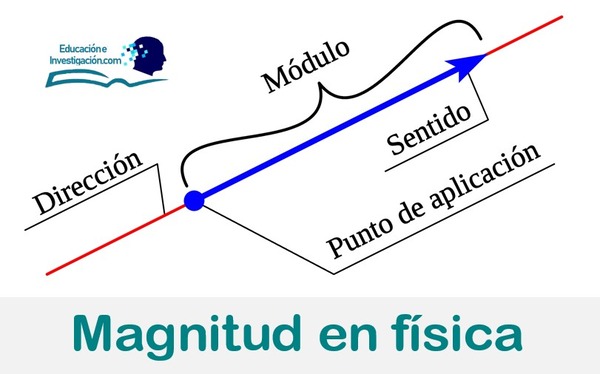
Las magnitudes vectoriales son aquellas que utilizan flechas o vectores para representarlas. Ejemplos de este tipo de magnitudes son la velocidad, la aceleración o las fuerzas.
Producto de un escalar por un vector
– De módulo el producto del número con el módulo del vector.
– Dirección del vector.
– Dirección, idéntica a la del vector si el número es positivo y opuesta si es negativo.
Si multiplicas un número por un vector, obtienes otro vector con la misma dirección y sentido que el primero si el número es positivo, pero mayor o menor. O un vector que es mayor o menor y apunta en la dirección opuesta al vector dado si el número es negativo.
Suma de vectores
Si sumas dos vectores, obtienes otro vector. Para obtener la suma de los vectores, hay que respetar la llamada «regla del paralelogramo«.
Se construye un paralelogramo cuyos lados son los vectores y se traza su diagonal para obtener la suma de los vectores.
Sustracción de vectores
Si restas dos vectores como en la suma, obtienes otro vector. Se puede utilizar la regla del paralelogramo para obtener el vector resta o diferencia. Sin embargo, hay que tener en cuenta que la diferencia puede considerarse como la suma de un vector y su opuesto.
Componentes de un vector
Siempre se puede descomponer un vector en sus dos componentes. Es decir, obtenemos otros dos vectores perpendiculares entre sí que, si actúan al mismo tiempo, tienen el mismo efecto que el vector considerado actuando solo.
Para realizar esta descomposición, necesitamos trazar una paralela al eje X y luego una paralela al eje Y. De esta forma obtenemos las componentes X e Y. De esta forma obtenemos las componentes X e Y.
Expresión de un vector en función de vectores unitarios
Si se puede aplicar el concepto de producto de un escalar por un vector, se obtiene una notación. Esto es muy útil para la representación de vectores.
Primero tenemos que definir lo que se denominan vectores unitarios. Es decir, vectores que tienen módulo uno (1) y cuya dirección es igual a la dirección de los ejes de coordenadas.
Además, su dirección es igual a la dirección positiva de los ejes de coordenadas.
Con la ayuda de estos vectores, es muy fácil escribir vectores cuya dirección sea la misma que la de los ejes de coordenadas.
>> Te recomiendo la lectura sobre las interacciones en física:
Interacciones, Leyes de Newton y Ejercicios de Fuerzas para 1er año de Ciencias




